Statisztikus fizika gyakorlat
"Közérdekű" kérdések és válaszok fermionokról és a kémiai potenciáljukról
Amikor a hideg fermionokról beszéltünk, és felrajzoltuk azt a lépcső függvényt, utána szóba került, hogy amikor E = μ, akkor a függvényérték mindig, minden T hőmérséklet mellett 1/2 az eloszlás alapján. És ezért ez egy fix pontja a függvénynek, hogy az E = μ0 esetén 1/2-et vesz fel magasabb hőmérsékleten is, csak a lépcsőfüggvény egyre jobban "lekerekedik". De akkor ezt azt jelenti, hogy μ értéke minden hőmérsékleten ugyanannyi, mint T = 0-ban? Mert gondolom a Fermi-eloszlásba mindig az aktuális μ-t kell beírni, és erről szó is volt, hogy hidegben lehet μ pozitív, hiszen az entrópia nem nő a részecske bejövetelével, de melegben viszont negatívnak kell lennie a kémiai potenciálnak, hogy állandó értéken maradjon az entrópia. Akkor viszont a hőmérséklet emelkedésével nem tolódik el a görbe (μ, 1/2) pontja is a negatívok felé?
De bizony eltolódik, tehát a videóban hallható fixpontos szöveg az szigorúan csak akkor igaz, amikor μ értékét fixen tartjuk valahogy, miközben változtatjuk a hőmérsékletet. (Ami adott részecskeszám esetén nyilván nem lehetséges.) Amiért mégis bennehagytam a "fixpontos" szöveget, az azért van, mert μ értéke az alacsony hűmérsékleti tartományban nagyon-nagyon lassan változik. Ezt az alábbi ábra szemlélteti. Ez az f(E)ω(E) függvény, vagyis az f(E) "lépcsős" Fermi-Dirac betöltöttségfüggvénynek és a gyökös ω(E) egyrészecske-állapotsűrűségnek a szorzatát mutatja a nemrelativisztikus esetben. (Forrás: Kubo, Statistical mechanics).
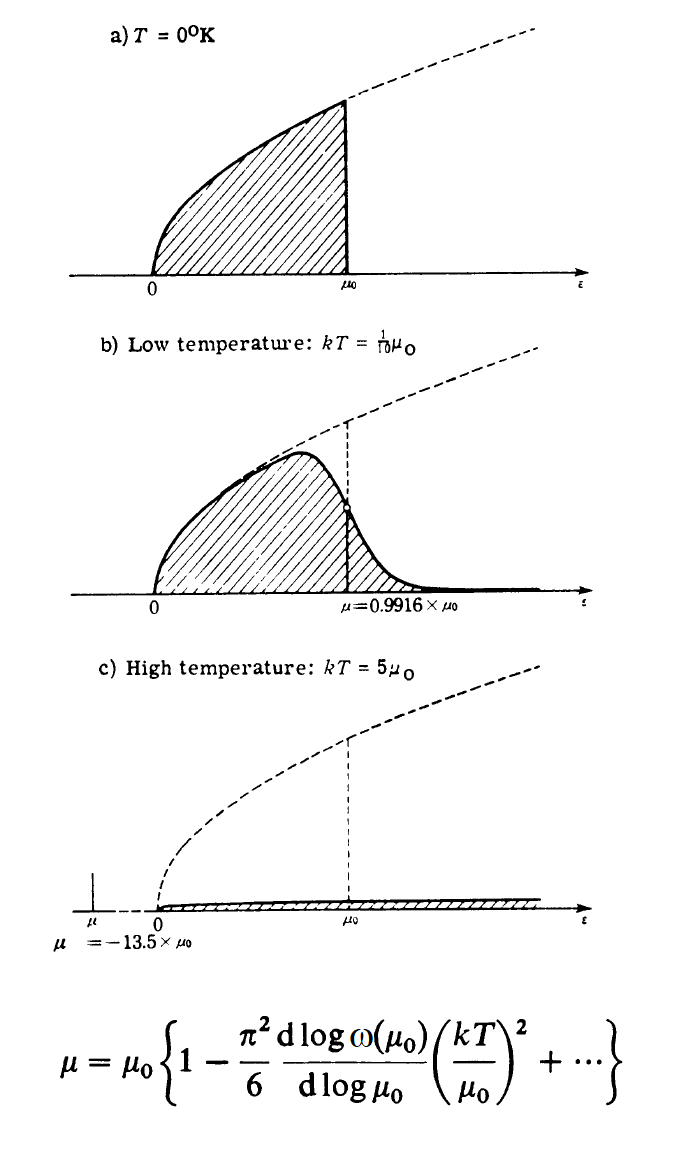
A satírozott rész, vagyis a görbe alatti terület így megadja az N részecskeszámot (hiszen ne feledjük, ferminokról lévén szó minden állapotot egy részecske tölthet be). A grafikonok alatt fel van tűntetve, hogy milyen értéknél helyezkedik el az aktuális μ, az alacsonyhőmérsékleti sorfejtést pedig a kép alján látható képlet mutatja. Látható, hogy még akkora hőmérsékleten is, amelyre kT értéke a nulla hőmérsékletű kémiai potenciál (vagyis Fermi-energia) egytizede, ott is csak egy százaléknyi a μ értékének változása μ0-hoz képest. Viszont az olyan hőmérsékletekre, amelyekre kT összemérhető μ0-lal, ott már nagyon mást kezdünk látni (c panel, ahol kT = 5 μ0).
Hasonló kérdés merült fel bennem egyébként a beadós 3. feladata kapcsán, hogy hogyan is kell érteni azt, hogy meghatározzuk az elektrongáz T = 0-hoz tartozó kémiai potenciálját, de utána kiszámoljuk, hogy ehhez az energiaszinthez tartozó hőmérséklet több ezer kelvin. Erre nem sikerült rájönnöm, hogy akkor valójában milyen hőmérsékleten van az elektrongáz, 0 kelvinen vagy melegebben, vagy mi oldja fel ezt a számomra ellentmondásosnak tűnő helyzetet.
Az ellentmondás feloldása, hogy itt a kiszámított több ezer kelvines érték, ami tehát nem más, mint μ0/k az éppen arra vonatkozik, hogy mi az a hőmérséklet, amelyre fölhevítve a rendszert már lényegében teljesen "kilapulna" az emlegetett lépcsőfüggvény. Nagyjából ezen a hőmérsékleten állna elő a μ = 0 helyzet. Ennek a kiszámítása tehát azért jó nekünk, mert ebből állapíthatjuk meg, hogy a nekünk érdekes hőmérséklettartományban (pl. 300 K) használhatjuk-e a fenti "alacsonyhőmérsékleti" közelítést. (S ha valóban tízezer kelvinek jönnek ki, akkor az derül ki, hogy igen.)
Illetve a feladat még megkérdezi, hogy van-e esélyünk ideális gázként látni az elektronokat, ezt a hőmérséklet alapján lehet megválaszolni, vagy a kémiai potenciál pozitivitása az, ami döntő?
Az előzőek alapján azt mondhatjuk, hogy azért nem láthatjuk ideális gázként nyüzsögni az elektronokat, mert a hőmérséklet mifelénk sokkal alacsonyabb, mint a Fermi-hőmérséklet, vagyis μ0/k. (És éppen ezért a kémiai potenciál is lényegében majdnem μ0.)
Gondolatok a "klímaszkepticizmusról"
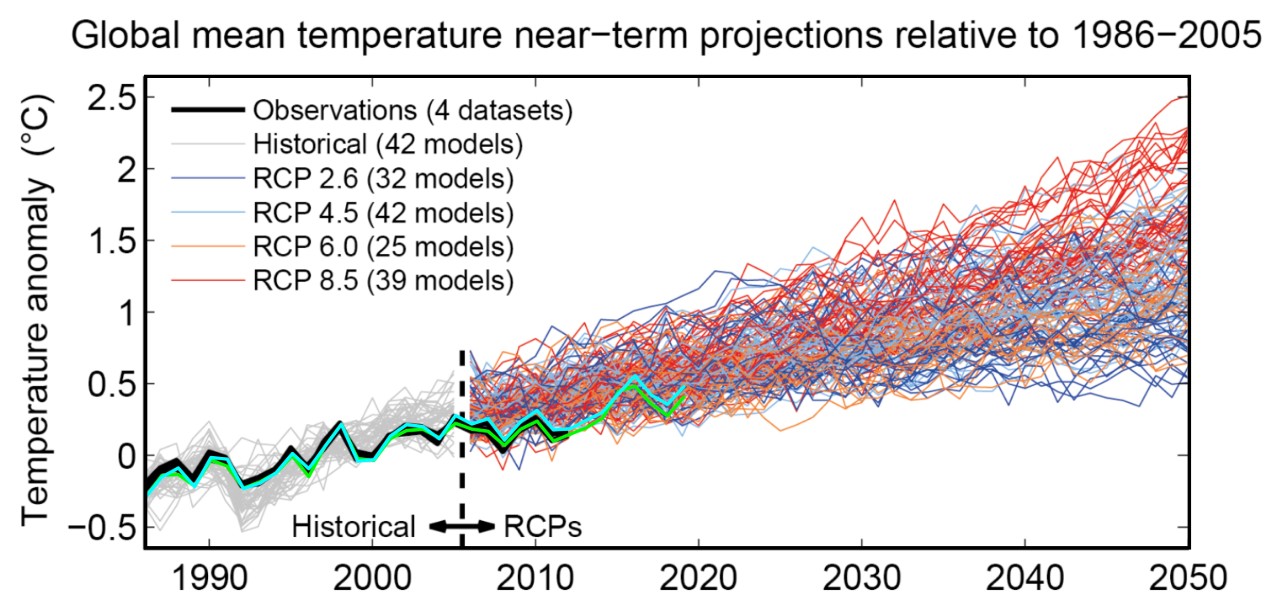
Nem tudom pontosan, hogy az Interneten gyülekező klímaszkeptikus összesküvéshívők milyen érvekkel jönnek elő mostanában vélt igazuk alátámasztására. Én egyáltalán nem tartom magam klímaszkeptikusnak és nem is igazán értem, hogy mit jelent az. Nagyon meggyőző bizonyítékok sokasága támasztja alá, hogy a Föld éghajlata változóban van és hogy ennek jelenlegi alakulása nem csupán természetes folyamat, nem intézhető el kizárólag a "nem tehetünk mi itt kérem semmiről, csak épp jövünk kifelé a Jégkorszakból" mantrával. Ez világos. Viszont most azt szeretném megmutatni, hogy a klímaváltozás megértésének mélysége jelenleg még messze nem közelíti azt a szintet, mint mondjuk a "modern" (értsd: száz éves) fizika elméletei, vagy épp az evolúcióelmélet, amelyeket persze szintén támadnak önjelölt szakemberek az Internet bugyraiban. Ezért nem tartom méltányosnak, hogy a közbeszédben a "klímatagadókat" (climate change deniers) élből ugyanabba a skatulyába pakoljuk, ahol a laposföld-hívők, kreacionisták, holdraszállástagadók és hasonlók tömörülnek. (Jómagam amúgy Balatontagadó vagyok.) De azért még mindig sokkal jobban tesszük, ha hallgatunk a klímakutatókra.
Online statisztikus fizika gyakorlat S01E07 (évadzáró)
Lokalizált spinek, vastapsok, járványok
Elkészült a félév utolsó epizódja! Ezúttal a kölcsönható részecskerendszerek, fázisátalakulások és egyebek világában mélyedünk el, megmutatva, hogy a statisztikus fizika eszköztárával akár bonyolultnak tűnő társadami folyamatokat is modellezhetünk. Illetve mindezek előtt egy kis "önök kérték" rovat a foton impulzusáról és arról, hogy hogyan is lesz az einsteini energiaképletből határesetben a jól ismert newtoni mozgási energia. Több beadandó nincs!
Köszönöm az egész féléves kitartó figyelmet mindenkinek!
Online statisztikus fizika gyakorlat S01E06
Bozonok, fotongáz és az ősrobbanás
Íme az újabb adag statisztikus fizika a végén egy kicsi kozmológiai kitekintéssel. Így a félév vége felé közeledve (és tekintettel arra, hogy még mindig sok beadandó "van kint") csak egy szorgalmi feladatot adnék. A vállalkozó kedvűek megkereshetnék, hogy honnan jön az előjelhibám a fotongáz állapotegyenletének levezetése során, amit a videóban is említettem, de nem jöttem rá. :) (UPDATE: persze közben rájöttem. 36:40 körül az ln(1-izé) deriválásakor az "izé" belső függvény deriváltjáról lemaradt egy minusz előjel, szóval semmi érdekes, ebből nem lesz Nobel-díj.) A feladatpontszámok frissítésével még várok egy kicsit, hiszen az elmúlt két napban hirtelen jó sok megoldás érkezett be és nagyon úgy tűnik, hogy még jön több is.
Online statisztikus fizika gyakorlat S01E05
A nagykanonikus állapotösszeg és a kvantumstatisztikák
Ez az adag kicsit lassabban készült el a tervezettnél, de cserébe hosszabb lett. Szét is szedtem egy elméletibb jellegű bevezetőre és a konkrét új példasor megbeszélésére. Az első videóval érdemes kezdeni, de aki már mindent tud a témában (pl. az előadásról), az nyugodtan átugorhatja. Íme:
A második videó pedig a feladatokkal kapcsolatos. Amit kérnék beadni, azok a következő kis dolgok:
- Az 1. feladat utolsó kérdése, vagyis a d = 1 és 2 dimenzióra vonatkozó eset.
- A 2. feladat második (energiás) integráljának kiszámítása.
- A 3. feladat behelyettesítős része, vagyis a Fermi-hőmérséklet meghatározása. (Megj.: a Fermi-hőmérséklet nem más, mint a Fermi-energia leosztva a Boltzmann-állandóval E = kT szellemében.)
Kellemes és hasznos időtöltést kívánok!
Kiegészítő megjegyzés (és korrekció) a IV/1. példához
"Ma is tanultunk valamit."
Az S01E04 jelű epizódban vétettem egy hibát a fajhő felírásában, nevezetesen 56 perc körül, amikor ez látható a táblán.
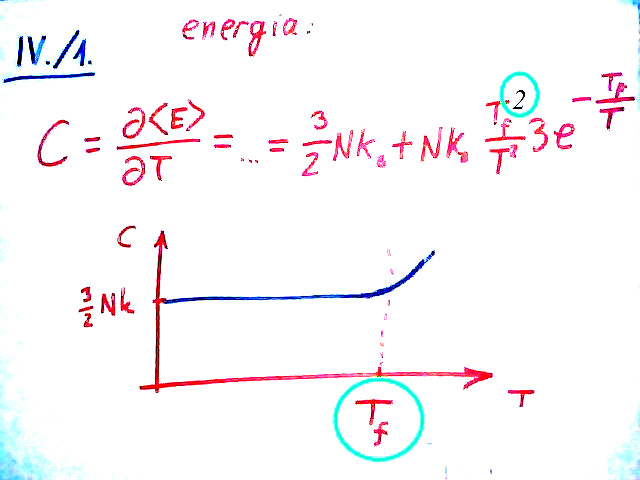
Itt két érdekesség is van. Az első egy szimpla elírás, ami számolás nélkül, pusztán dimenzióanalízissel belátható: a felírt eredeti képlet nem helyes, lemaradt a forgási hőmérséklet hatványkitevője. Most ideírtam feketével és jól bekereteztem zölddel. (Illetve megjegyzendő, hogy a képlet nem jön ki csupán csak az <E> deriválásából, hanem még szükséges ehhez az egyszerűbb alakhoz a T << Tf feltételezése is.)
Ez egy egyszerű elírás, sajnos biztos maradt benne több is. (Mindig van, mindenki járjon nyitott szemmel és gyanakodjon, ahogy FWK2EN is tette ezúttal, köszönet érte!) A második viszont tényleg érdekes, és a rajzocskát érinti. Nem hagyott nyugodni, így gyorsan írtam egy egyszerű programot, ami kiszámolja nekem a rotációs állapotösszeget, azaz ezt:
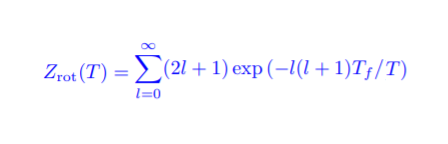
No persze nem végtelenig szummázva, hanem egy általam megadott tetszőleges "lmax" értékig, majd szépen veszi a logaritmusát, megszorozta a T hőmérséklet négyzetével és végül (egyszerű differenciaszámítással) "lederiválja", pont a legutóbbi videóban tárgyalt képletek szerint. Tf, N és k értékét egységnyinek választottam, vagyis ez azt jelenti, hogy a hőmérsékletet a mindenkori Tf-egységekben, a C fajhőt pedig Nk egységekben kapjuk meg. Attól függően, hogy az lmax értékét – vagyis azt, hogy a szummában medig megyek el – hogyan választom meg, más-más közelítő C(T)-függvényeket kapok. Az eredmények így festenek:
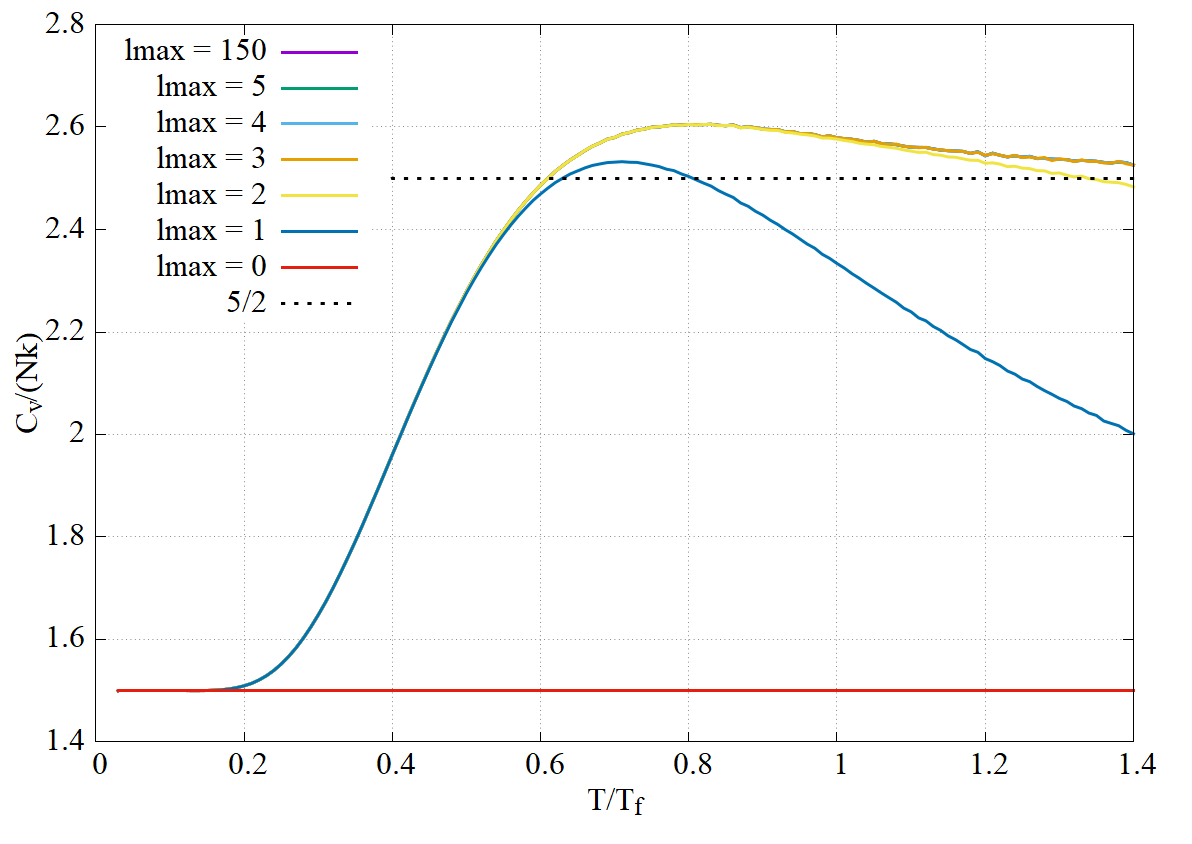
A tanulságok a következők:
- "Látjuk, hogy nem látjuk" az lmax = 3 fölötti értékekhez tartozó görbéket. Ez azért van, mert ezek ennyire együtt mennek, a görbék letakarják egymást. Vagyis a képlet gyorsan konvergál: a rajzon mutatott tartományban az lmax = 3 és az lmax = 150 lényegében ugyanazt a görbét adja, az eltérés a vonalvastagságnál kisebb.
- Azt is látjuk viszont, hogy az lmax = 1 görbe még nagyon mást művel. Ez nem más, mint a IV/1 feladat szerinti közelítés, amiben csak a sorfejtés második tagjáig megyünk el. Persze kicsi T-értékekre azért jól működik. Ezért is lehet indokolt a fajhőképlet további egyszerűsításe, hiszen pontosan abban a tartományban, amiben még megfelelő értéket ad (mondjuk T/Tf = 0.4-ig) addig valóban jól helyettesíthető ez a függvény a kijavított táblaképen szereplő formulával, az afölötti hőmérsékleteken pedig már amúgy is mindenképpen rossz becslést ad az lmax = 1 közelítés.
- De a legfontosabb, ami az egész posztot ihlette: a videóbeli tábrarajz teljesen rossz helyre jelöli Tf értékét! Amint látjuk, ott (érzésre) azt rajzoltam, hogy a görbe "felkunkorodása" Tf környékén kezdődik, de az igazi grafikonok egyértelműen mutatják, hogy ez az ominózus felkunkorodás már 0.2Tf környékén megtörténik!
- És még egy: emlegettem a videóban, hogy a rotációs fajhő "túllő", vagyis van egy maximuma, majd visszacsökken és csak utána tart a IV/2. példában kiszámolt C = 5/2 Nk értékhez. Ez is jól látható a ploton.
Online statisztikus fizika gyakorlat S01E04
Egyenlők és egyenlőbbek, avagy amikor bedől az ekvipartíció
Az új gyakorlat megtekinthető alább, a feladatsor pedig itt. A megoldandó apró kis feladatok a következők:
- Az 1. és 3. feladatban a konkrét számértékekre vonatkozó kis számítások, vagyis a keresett Tf és Tr hőmérsékleti értékek.
- Illetve a 4. feladat (ezek szintén nagyságrendi becslések).
Kellemes időtöltést!
Kis megjegyzés a III/1. feladathoz
"FYI" rovat
Sokan kihozták a teljesen helyes fajhőt (vagyis ügyesen deriválták az energia átlagát) a III/1-es feladatban, viszont szomorkodtak, hogy nem lett benne a végeredményben semmilyen formában a ch-függvény. Természetesen ezért nem jár pontlevonás, nem matekórán vagyunk. Valószínűleg az lehet az ok, hogy a köztudatban nincsenek benne a hiperbolikus függvényekre vonatkozó addíciós tételek, meg kétszeres és félszögekre vonatkozó összefüggések. Ezek hasonlítanak a trigonometrikus függvények analóg képleteire. Ami most itt jól jöhetett volna, az (a ch-függvény exponenciálisos felírásán túl) az az alábbi varázslatos összefüggés. Ezzel belátható, hogy a végeredmény egy 1/ch alakú függvény négyzetével arányos. :)
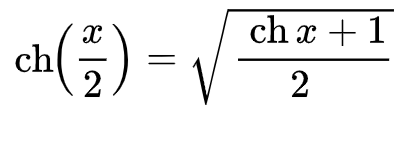
Online statisztikus fizika gyakorlat S01E03
A kanonikus állapotösszeg további rejtelmei
Íme az újabb gyakorlati anyag, előtte pedig néhány "napirend előtti" pont a feladatok értékeléséről és egy felmerült kérdésről. Az aktuális feladatsor továbbra is ez. Ezúttal két egyszerű feladat megoldását kérném a szokott módon. Ezek:
- a 6-os feladat
- és a 9-es feladat
Jó szórakozást! :)