Amikor a hideg fermionokról beszéltünk, és felrajzoltuk azt a lépcső függvényt, utána szóba került, hogy amikor E = μ, akkor a függvényérték mindig, minden T hőmérséklet mellett 1/2 az eloszlás alapján. És ezért ez egy fix pontja a függvénynek, hogy az E = μ0 esetén 1/2-et vesz fel magasabb hőmérsékleten is, csak a lépcsőfüggvény egyre jobban "lekerekedik". De akkor ezt azt jelenti, hogy μ értéke minden hőmérsékleten ugyanannyi, mint T = 0-ban? Mert gondolom a Fermi-eloszlásba mindig az aktuális μ-t kell beírni, és erről szó is volt, hogy hidegben lehet μ pozitív, hiszen az entrópia nem nő a részecske bejövetelével, de melegben viszont negatívnak kell lennie a kémiai potenciálnak, hogy állandó értéken maradjon az entrópia. Akkor viszont a hőmérséklet emelkedésével nem tolódik el a görbe (μ, 1/2) pontja is a negatívok felé?

De bizony eltolódik, tehát a videóban hallható fixpontos szöveg az szigorúan csak akkor igaz, amikor μ értékét fixen tartjuk valahogy, miközben változtatjuk a hőmérsékletet. (Ami adott részecskeszám esetén nyilván nem lehetséges.) Amiért mégis bennehagytam a "fixpontos" szöveget, az azért van, mert μ értéke az alacsony hűmérsékleti tartományban nagyon-nagyon lassan változik. Ezt az alábbi ábra szemlélteti. Ez az f(E)ω(E) függvény, vagyis az f(E) "lépcsős" Fermi-Dirac betöltöttségfüggvénynek és a gyökös ω(E) egyrészecske-állapotsűrűségnek a szorzatát mutatja a nemrelativisztikus esetben. (Forrás: Kubo, Statistical mechanics).

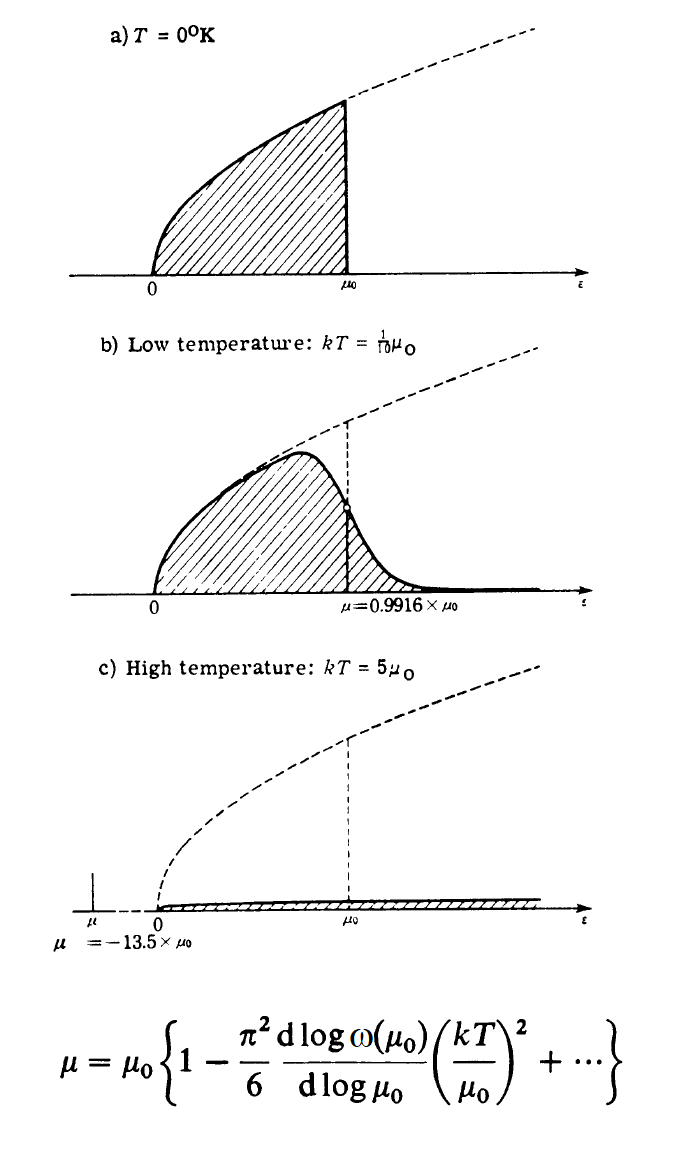
A satírozott rész, vagyis a görbe alatti terület így megadja az N részecskeszámot (hiszen ne feledjük, ferminokról lévén szó minden állapotot egy részecske tölthet be). A grafikonok alatt fel van tűntetve, hogy milyen értéknél helyezkedik el az aktuális μ, az alacsonyhőmérsékleti sorfejtést pedig a kép alján látható képlet mutatja. Látható, hogy még akkora hőmérsékleten is, amelyre kT értéke a nulla hőmérsékletű kémiai potenciál (vagyis Fermi-energia) egytizede, ott is csak egy százaléknyi a μ értékének változása μ0-hoz képest. Viszont az olyan hőmérsékletekre, amelyekre kT összemérhető μ0-lal, ott már nagyon mást kezdünk látni (c panel, ahol kT = 5 μ0).

Hasonló kérdés merült fel bennem egyébként a beadós 3. feladata kapcsán, hogy hogyan is kell érteni azt, hogy meghatározzuk az elektrongáz T = 0-hoz tartozó kémiai potenciálját, de utána kiszámoljuk, hogy ehhez az energiaszinthez tartozó hőmérséklet több ezer kelvin. Erre nem sikerült rájönnöm, hogy akkor valójában milyen hőmérsékleten van az elektrongáz, 0 kelvinen vagy melegebben, vagy mi oldja fel ezt a számomra ellentmondásosnak tűnő helyzetet.

Az ellentmondás feloldása, hogy itt a kiszámított több ezer kelvines érték, ami tehát nem más, mint μ0/k az éppen arra vonatkozik, hogy mi az a hőmérséklet, amelyre fölhevítve a rendszert már lényegében teljesen "kilapulna" az emlegetett lépcsőfüggvény. Nagyjából ezen a hőmérsékleten állna elő a μ = 0 helyzet. Ennek a kiszámítása tehát azért jó nekünk, mert ebből állapíthatjuk meg, hogy a nekünk érdekes hőmérséklettartományban (pl. 300 K) használhatjuk-e a fenti "alacsonyhőmérsékleti" közelítést. (S ha valóban tízezer kelvinek jönnek ki, akkor az derül ki, hogy igen.)

Illetve a feladat még megkérdezi, hogy van-e esélyünk ideális gázként látni az elektronokat, ezt a hőmérséklet alapján lehet megválaszolni, vagy a kémiai potenciál pozitivitása az, ami döntő?

Az előzőek alapján azt mondhatjuk, hogy azért nem láthatjuk ideális gázként nyüzsögni az elektronokat, mert a hőmérséklet mifelénk sokkal alacsonyabb, mint a Fermi-hőmérséklet, vagyis μ0/k. (És éppen ezért a kémiai potenciál is lényegében majdnem μ0.)