Már itt is van a következő (kilencedik) adag kvantumgyak.

Itt a várva-várt újabb adag! A vadonatúj kis feladatsor (immár értelmezhető karakterekkel) pedig megtalálható a Teamsben. Jó szórakozást! :) Megj.: 2:42-nél "le-Hamilton-terezem" a Hilbert-teret, ne hagyjátok Magatokat megtéveszteni! Csak megkavart ez a sok H betű. :P

Megjött az új gyakorlat videója! A mérés rejtélyének megtárgyalásakor (19-20. perc körültől) vétettem egy nagy hibát. Leírtam és sajnos el is mondtam, hogy a Hamilton-operátort ráhattatjuk egy tetszőleges Φ függvényre, majd az operáció eredményeként kapott θ függvényt fejtjük ki a ψi sajátfüggvények szerint. Ezt így írtam:

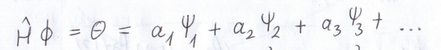
Ezt persze megtehetjük, de az így kapott az ai kifejtési együtthatókra akkor nem lesz igaz az a 24. perc környékén elhangzó állítás, mely szerint "ezek négyzete adja majd meg az adott állapot bekövetkezésének valószínűségét". A helyes felírás simán csak ez lett volna:

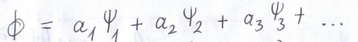
Vagyis mindenféle operátor-hattatás nélkül felbontjuk a Φ függvényünket a ψi sajátfüggvények, vagyis a Hamilton-operátor sajátfüggvényei szerint. Ekkor és csak ekkor igaz, hogy a kifejtási együtthatók azt számszerűsítik (ahogy a húrnál is volt), hogy a Φ függvényünk melyik ψi sajátfüggvényre milyen mértékben hasonlít, s ezért lesz az együtthatók négyzete az adott sajátállapot bekövetkezésének valószínűsége. A kérdés további tisztázására a következő gyakon még visszatérek. De az két hét múlva lesz. Addig nincsen új házi feladat, hiszen lesz helyette a szünet idejére jó kis Károlyházy-verseny, amiről hamarosan itt lehet tájékozódni (feladatkihirdetés október 22-én, online beküldési határidő: november 2). Mindenkinek nagyon ajánlom a részvételt!

Itt megtekinthető a legújabb gyakorlat. Az új példasor pedig elérhető a MS Teams felületen a "Course materials" mappában. :)

A vadonatúj gyakorlat itt tekinthető meg:

Mátrixok, sajátértékek, sajátvektorok, ortogonalitás valós és komplex esetben. Jó szórakozást! :)

Íme az újabb adag. Golyók, rugók, mátrixok. A feladatsor  pedig elérhető a Teamsben! 

A mai kvantummechanika gyakorlaton NEM esett szó kvantummechanikáról. Viszont rezgő húrokról annál több. Beadandó egyelőre még nincs, de szerintem jövő héten már lesz. Sajnos a rögzített videóban jó sok hanghiba keletkezett. :(

Tóth Kristóf jóvoltából ajánlanék továbbá egy jó kis Fourier-kifejtéses szemléltetőprogramot emberbarát grafikus kezelőfelülettel, ami innen érhető el. Ezt a programot is meg lehet kérni, hogy tetszőleges pontossággal "kikeverje" szinuszokból például a gyakorlaton szereplő háztető-alakot. Kristóf a bizonyára sokak által ismert Geogebra appban ki is plotolta az első öt Fourier-komponenst, illetve összegüket (vastag piros vonal), amely máris egész szépen kirajzolja a háztetőt, pedig ez még csak egy öttagú közelítő összeg. A komponensek súlyfaktorait (amplitúdóit) a bal oldali "algebra ablakban" olvashatjuk.

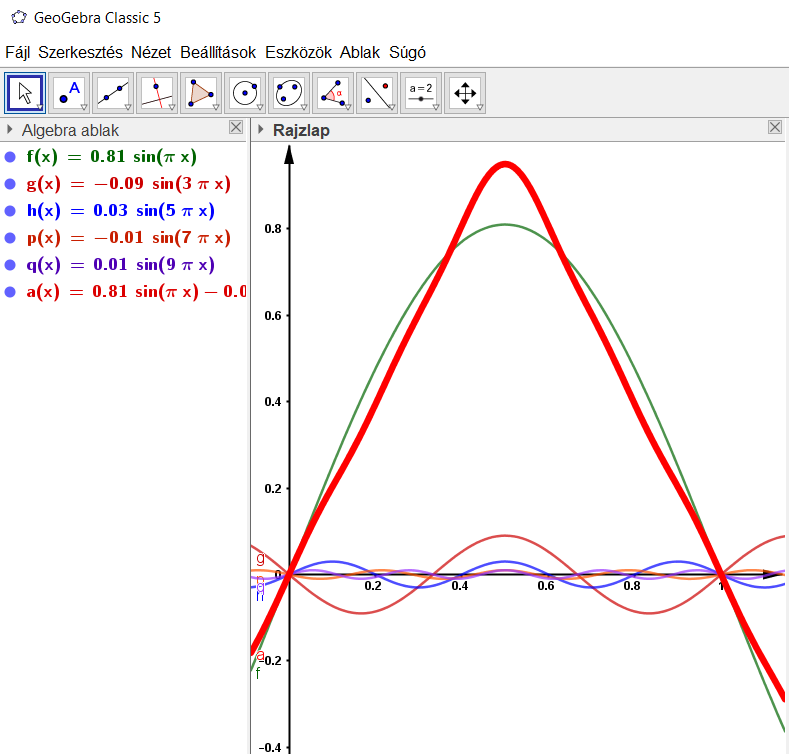
Továbbá a szinuszfüggvények órán említett ortogonalitása is tesztelgethető például a Wolfram Alpha segítségével, ahogyan azt Kristof is tette emitt. (Köszönöm! :) )  Amúgy sem árt játszadozni a Wolframmal, hiszen később is jól fog jönni. Jó szórakozást!

Bevezető gondolatok arról, hogy miért érdemes kvantummechanikát tanulni, illetve egy kis bevezetés az operátorok és a sajátértékproblémák világába. Tóth Kristóf említett TDK-dolgozata elérhető itt.