Megjött az új gyakorlat videója! A mérés rejtélyének megtárgyalásakor (19-20. perc körültől) vétettem egy nagy hibát. Leírtam és sajnos el is mondtam, hogy a Hamilton-operátort ráhattatjuk egy tetszőleges Φ függvényre, majd az operáció eredményeként kapott θ függvényt fejtjük ki a ψi sajátfüggvények szerint. Ezt így írtam:

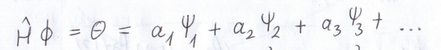
Ezt persze megtehetjük, de az így kapott az ai kifejtési együtthatókra akkor nem lesz igaz az a 24. perc környékén elhangzó állítás, mely szerint "ezek négyzete adja majd meg az adott állapot bekövetkezésének valószínűségét". A helyes felírás simán csak ez lett volna:

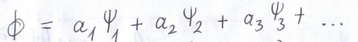
Vagyis mindenféle operátor-hattatás nélkül felbontjuk a Φ függvényünket a ψi sajátfüggvények, vagyis a Hamilton-operátor sajátfüggvényei szerint. Ekkor és csak ekkor igaz, hogy a kifejtási együtthatók azt számszerűsítik (ahogy a húrnál is volt), hogy a Φ függvényünk melyik ψi sajátfüggvényre milyen mértékben hasonlít, s ezért lesz az együtthatók négyzete az adott sajátállapot bekövetkezésének valószínűsége. A kérdés további tisztázására a következő gyakon még visszatérek. De az két hét múlva lesz. Addig nincsen új házi feladat, hiszen lesz helyette a szünet idejére jó kis Károlyházy-verseny, amiről hamarosan itt lehet tájékozódni (feladatkihirdetés október 22-én, online beküldési határidő: november 2). Mindenkinek nagyon ajánlom a részvételt!