Első adag:

Második adag:

Első felvonás:

Második felvonás:

Végre ténylegesen elkezdjük a statfizt. Állapotösszeg dobozban pattogó részecskére és oszcillátorra. De beadandó feladat még nincs.

Első adag:

Második adag:

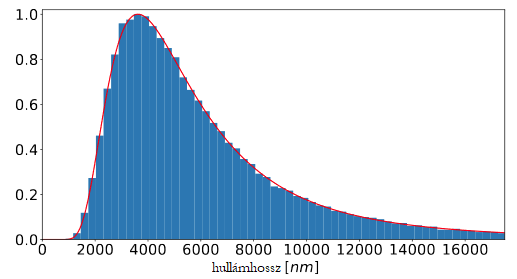
Felmerült a legutóbbi órán a "hol van a napsugárzás spektrumának csúcsa" kérdéskör. A válasz, ahogy mondtam is: attól függ.  Itt van mindehhez egy gyors és remélhetőleg szemléletes kis kiegészítés.

A feketetest-sugárzási spektrum, és úgy általában, mindenféle spektrum sűrűségfüggvény. Ez azt jelenti, hogy amit leolvasunk róla, azt így kell értelmezni: milyen valószínűséggel (gyakorisággal, arányban, mértékben, stb.) mér(het)ek az adott x értékhez tetszőlegesen közeli adatot. A "tetszőlegesen közeli" most nem csak a szokásos matematikusi precízkedés, hanem egy nagyon fontos elem, amint majd látni fogjuk. A dolgot elképzelhetjük úgy is, hogy mérünk valamit (pl. a beérkező fotonok energiáját egy fényforrásból) és készítünk egy hisztogramot arról, hogy a különböző hullámhosszú fotonból mennyi érkezett be, majd a darabszámukat megszorozva az energiájukkal megkaphatunk valamiféle fényintenzitással arányos mennyiséget. Persze mérőműszerünkben a hullámhosszat csak bizonyos felbontással tudjuk mérni, így azokat a beütéseket egy kalap alá vesszük, amelyeknek hullámhossza a vizsgált λ-érték bizonyos dλ sugarú környezetébe esik. Ebből a "dobozolásból" (angolul "binning") elég sok mérés esetén összejöhet egy ilyen hisztogram (kék). Ez amúgy nem a napspektrum, hanem egy hidegebb feketetest esete épp (a hőmérséklet plusszpontért megbecsülhető és emailben elküldhető nekem). Az elméleti Planck-törvényt a piros görbe mutatja. Megjegyzés: ez nem egy igazi kísérletből van, hanem egy szimulációból, forrása ez).