Felmerült a legutóbbi órán a "hol van a napsugárzás spektrumának csúcsa" kérdéskör. A válasz, ahogy mondtam is: attól függ.  Itt van mindehhez egy gyors és remélhetőleg szemléletes kis kiegészítés.

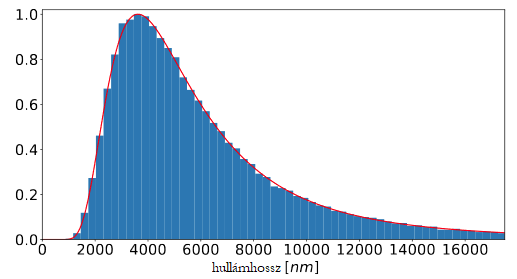
A feketetest-sugárzási spektrum, és úgy általában, mindenféle spektrum sűrűségfüggvény. Ez azt jelenti, hogy amit leolvasunk róla, azt így kell értelmezni: milyen valószínűséggel (gyakorisággal, arányban, mértékben, stb.) mér(het)ek az adott x értékhez tetszőlegesen közeli adatot. A "tetszőlegesen közeli" most nem csak a szokásos matematikusi precízkedés, hanem egy nagyon fontos elem, amint majd látni fogjuk. A dolgot elképzelhetjük úgy is, hogy mérünk valamit (pl. a beérkező fotonok energiáját egy fényforrásból) és készítünk egy hisztogramot arról, hogy a különböző hullámhosszú fotonból mennyi érkezett be, majd a darabszámukat megszorozva az energiájukkal megkaphatunk valamiféle fényintenzitással arányos mennyiséget. Persze mérőműszerünkben a hullámhosszat csak bizonyos felbontással tudjuk mérni, így azokat a beütéseket egy kalap alá vesszük, amelyeknek hullámhossza a vizsgált λ-érték bizonyos dλ sugarú környezetébe esik. Ebből a "dobozolásból" (angolul "binning") elég sok mérés esetén összejöhet egy ilyen hisztogram (kék). Ez amúgy nem a napspektrum, hanem egy hidegebb feketetest esete épp (a hőmérséklet plusszpontért megbecsülhető és emailben elküldhető nekem). Az elméleti Planck-törvényt a piros görbe mutatja. Megjegyzés: ez nem egy igazi kísérletből van, hanem egy szimulációból, forrása ez).

No már most képzeljük el, hogy nem a hullámhossz szerint, hanem a frekvencia (vagyis egy 1/λ-val arányos mennyiség) függvényében tudunk egyenletesen  "dobozolni", vagyis binelni. Például mert ilyen a mérési módszerünk. Íme ugyanaz a besugárzás, de most az f frekvencia szerint dobozolva:

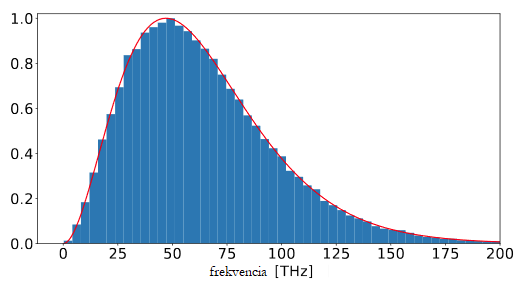
Állításom: mivel egy λ szerinti egyenletes felbontás f = c/λ szerint már egyáltalán nem egyenletes dobozolás, ezért a két hisztogram csúcsa biztosan nem esik egybe, abban az értelemben, hogy ha az első verzió csúcsa egy adott λ* értéknél helyezkedik el, akkor a második csúcsa biztosan nem az f = c/λ*-nál lesz.

Miért is? Mert mindaz a sok "beütés", ami mondjuk λ kis értékeinél egyetlen 2·dλ-nyi dobozba került, jól megnövelve az ide tartozó intenzitást, az a frekvencia szerint szortírozva egy óriási frekvenciatartományon itt-ott szétszóródva jelentkezik majd. Ezért áll elő tehát az a helyzet, hogy a sűrűségfüggvényeket nem szabad "ész nélkül" az x tengelyen mért mennyiség átskálázásával transzformálni, hanem ahhoz az úgynevezett Jacobi-determinánst, vagyis az átskálázás paraméterét is figyelembe kell venni. A különbség elég látváyos tud lenni:

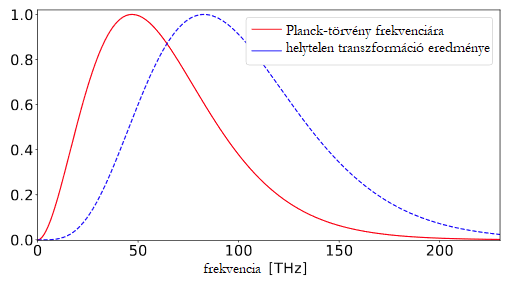
A nagyjából 6000 K-es napfelszínt fekete testként tekintve ez pl. arra vezet, hogy a hullámhossz függvényében ábrázolva a maximális intenzitás helyére λ* = 482.962 nm adódik (kék szín), amely f = 620.737 THz frekvenciának felel meg. Ugyanakkor ugyanezt frekvencia szerint paraméterezve a csúcs helyére f* = 352.735 THz-et kapunk, melyhez a λ = 849.907 nm-es hullámhossz (vörös) tartozik.

Hát már semminek sem hihet az ember? A helyzet azért nem olyan rossz. Tekintsük például a sűrűségfüggvényeink integrálját (primitívfüggvényét)! Ez annak felel meg, hogy nem azt vizsgálom, hogy milyen valószínűséggel esik a mérési eredményem az x érték dx sugarú tartományába, hanem azt, hogy milyen valószínűséggel mérek olyan értéket, ami az adott x-nél kisebb? Ez nyilván egy x szerint monoton növő függvényt (úgynevezett eloszlásfüggvényt) fog eredményezni, amit az alsó vázlatkám mutat.

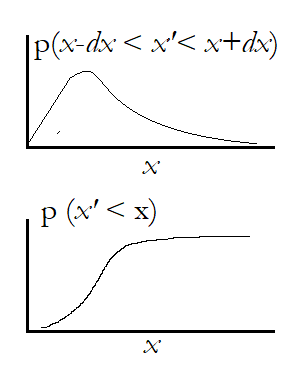
Ebben tehát már nincs szó "dobozolásról", vagyis ezt a függvényt nyugodtan transzformálhatjuk "ész nélkül", képezve például az y = 1/x új változót, vagy bármi mást. És ha ezzel megvagyunk, nincs más dolgunk, mint az így kapott úgy függvényt szépen újra lederiválni y szerint, s ebből már egy teljesen korrekt, helyes sűrűségfüggvény keletkezik.

Ez nem egy bonyolult dolog persze, de azért is írtam meg gyorsan ide, mert néha egészen komoly helyeken (szakmai cikkekben!) is látok példát arra, hogy a szerzők belefutnak ebbe a hibába. Nem árt tehát, ha észben tartjuk. :)

Ez meg itt egy kis történeti érdekesség: egy menő infografika 1944-ből elektromágneses hullámokról (maga a Nobel-díjas Arthur Compton tervezte, Somogyi Péter pedig megtalálta, köszönöm).